КОЛЕБАНИЯ
Спасибо нашим инвесторам из казино онлайн
КОЛЕБАНИЯ
, процессы (в наиболее общем смысле), периодически меняющие свое направление со временем. Процессы эти могут быть весьма разнообразными. Если напр. подвесить на стальной спиральной пружине тяжелый шар, оттянуть его и затем предоставить самому себе, то он будет совершать колебания под действием сил упругости. Таковы же упругие колебания струн, стержней и т. д. Колеблющейся величиной может быть однако и сила электрического тока (переменный ток) и напряжение электрического поля (электрические колебания) и т. д. Прототипом всякого К. может служить колебательное движение точки, т. е. движение ее взад и вперед по нек-рому отрезку прямой между двумя крайними положениями. Рассмотрим наиболее простое и вместе с тем наиболее важное колебательное движение— т. н. простое гармоническое К. Представим себе точку, равномерно обращающуюся по окружности радиуса
а
с периодом
Т.
Это значит, что если точка& р в некоторый момент вы –
/^~~\
~»\ шла из положения
М /
^Г’ТчтМ, (рис. 1), двигаясь напр. / SJ
/ \
против часовой стрел – /_____
Л
^\^\ \
ки, то через
Т
секунд NJ
у о
&
Им она вновь вернется в ту \
У
I
же точку. Рассмотрим gv-’-___В’
у
теперь движение про – ^-^___^ екции этой точки, напр.& q на вертикальный диа-& рис. 1. метр
PQ,
т. е. движение основания перпендикуляра, опущенного из точки на этот диаметр. Легко видеть, что в то время как точка, движущаяся по окружности против часовой стрелки, выйдя из
М,
совершает одно полное обращение, проекция совершает оДно полное К. по диаметру, к-рое состоит в движении от О к
Р,
затем обратно от Р к О, далее от
О
к
Q
и обратно к
О.
Так. обр. период обращения Т точки по окружности будет вместе с тем периодом полного К. проекции этой точки по диаметру. Величина, обратная
Т.
показывает очевидно, сколько полных колебаний совершается в единицу времени; она называется частотой К. и обозначается обычно грёч. буквой
v = – f.
Расстояние колеблющейся точки от начального положения
О
называется элонгацией; наибольшее же удаление колеблющейся точки от начального положения (О на рис. 1) характеризует размах К. и называется амплитудой. Состояние К. точки, т. е. ее положение на диаметре
PQ и
направление ее движения, вполне определяется положением вспомогательной точки, движущейся по окружности. Это последнее в свою очередь известно, если дан угол, составляемый радиусом, проведенным в данную точку, и каким-либо диаметром, принятым за начальный, например с горизонтальным диаметром
MN.
Этот угол, вполне определяющий состояние колебательного движения точки, называется фазой К. Напр. угол
МО А
будет фазой К. точки
А;
тупой угол
MOB
—фазой К. точки
В.
Если, как в данном случае, фазы отличаются на 180° (или, что то же, на
л),
то говорят, что точки находятся в противополож – ных фазах: в этом случае они расположены симметрично относительно точки
О
и двигаются в противоположных направлениях. В течение периода
Т
точка завершает полное К., вследствие чего ее фаза изменяется на целую окружность, или на
2л.
Ясно, что в любой момент
t
фаза колебания
& р
будет связана с периодом
Т
следующим отношением: – f – = -™, или
у
= 2тг-_ = 2
3zvt.
&
(1) Из рассмотрения треугольника
ААЮ
на основании правил тригонометрии непосредственно получается для элонгации
s
колеблющейся точки следующая формула:
s
=
О A
sin
& р
=
а
. sin 2
л
*г =
а
. sin 2 я v f, (2) где & Х4=а—амплитуда К. — Формула (2) представляет собой основной закон гармонического колебания. Т. к. величина синуса колеблется между значениями +1 и —1, то величина элонгации колеблется между
+а
и —а. Если графически изобразить зависимость между элонгацией и фазой, то получится кривая, изображенная На рис. 2. Эта
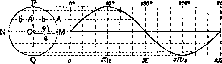
Рисунок 2.
кривая называется синусоидой, а потому и самое К. называется с и н у с о-и д а л ь н ы м. По сказанному вначале это относится не только к колебательному движению точки, но может относиться также и капр. к переменному электрическому току. Отсюда происхождение таких терминов, как «синусоидальные токи электротерапии».— Скорость точки, совершающей гармоническое К., не остается постоянной в течение периода. Действительно, в М и N точка на окружности и ее проекция двигаются параллельно друг к другу, а около Р и Q — почти перпендикулярно. Из этого следует, что гармонически колеблющаяся точка «обладает наибольшей скоростью, проходя через середину О отрезка, вдоль которого она двигается, и наименьшей—у концов этого отрезка; в Р и Q она на мгновение останавливается и вслед за тем меняет направление своего движения. Математически закон изменения скорости со временем выразится формулой u = -^cos2tt=- или, если вместо периода Т. ввести частоту v=Yf v = = 2 п v a cos 2 л v t. Т. к. при непрерывном ‘изменении угла косинус колеблется, как и синус, в пределах от +1 до — 1, то и скорость будет периодически изменяться, колеблясь между вели-2л а& 2яа чинами – f – и —„- . Ускорение (tv) так – же легко может быть найдено математически, и оно равно w = —^ sin ~ ; если мы сопоставим это выражение с формулой (2), то найдем w = — ™ s или, обозначая постоян – ную величину -=^ через к, получим w=—ks. Мы видим таким образом, что если точка колеблется гармонически, то ее ускорение направлено к центру (знак — в предыдущей формуле) и пропорционально элонгации, удалению от центра. Это свойство справедливо вообще и обычно служит критерием того, что данное колебательное движение является гармоническим. Наконец энергия колебания оказывается пропорциональной квадрату амплитуды. Гармоническое К. является наиболее важным потому, что по теореме Фурье любое периодическое движение может быть представлено как совокупность гармонических К. с различными амплитудами, но с частотами, относящимися, 1:2:3:4 (основной тон, октава, кварта, квинта и т. д.). Подобное разложение периодических движений является важным во многих практических применениях. Существуют приборы, позволяющие осуществлять это разложение механически (гармонические анализаторы). Лит.: Хвольсон О., Курс физики, том I, 1923. &Э. Шпольский.